Направление ускорения движении по окружности. Движение по окружности
При описании движения точки по окружности мы будем характеризовать перемещение точки углом Δφ , который описывает радиус-вектор точки за время Δt . Угловое перемещение за бесконечно малый промежуток времени dt обозначается dφ .
Угловое перемещение – величина векторная. Определяется направление вектора (или ) по правилу буравчика: если вращать буравчик (винт с правосторонней резьбой) в направлении движения точки, то буравчик будет двигаться в направлении вектора углового смещения. На рис. 14 точка М движется по часовой стрелке, если смотреть на плоскость движения снизу. Если крутить буравчик в этом направлении, то вектор будет направлен вверх.
Таким образом, направление вектора углового перемещения определяется выбором положительного направления вращения. Положительное направление вращения определяется правилом буравчика с правосторонней резьбой. Однако с таким же успехом можно было взять буравчик с левосторонней резьбой. В этом случае направление вектора углового смещения было бы противоположным.
При рассмотрении таких величин, как скорость, ускорение, вектор смещения не возникал вопрос о выборе их направления: оно определялось естественным образом из природы самих величин. Такие вектора называются полярными. Вектора, подобные вектору углового перемещения, называются аксиальными, или псевдовекторами . Направление аксиального вектора определяется выбором положительного направления вращения. Кроме того, аксиальный вектор не имеет точки приложения. Полярные векторы , которые мы рассматривали до сих пор, приложены к движущейся точке. Для аксиального вектора можно лишь указать направление (ось, axis – лат.), вдоль которой он направлен. Ось, вдоль которой направлен вектор углового смещения, перпендикулярна плоскости вращения. Обычно вектор углового перемещения изображают на оси, проходящей через центр окружности (рис. 14), хотя его можно нарисовать в любом месте, в том числе на оси, проходящей через рассматриваемую точку.
В системе СИ углы измеряются в радианах. Радиан – это такой угол, длина дуги которого равна радиусу окружности. Таким образом, полный угол (360 0) равен 2π радиан.
Движение точки по окружности
Угловая скорость – векторная величина, численно равная углу поворота за единицу времени. Обозначается обычно угловая скорость греческой буквой ω. По определению, угловая скорость – это производная угла по времени:
Направление вектора угловой скорости совпадает с направлением вектора углового перемещения (рис. 14). Вектор угловой скорости, так же, как и вектор углового перемещения, является аксиальным вектором.
Размерность угловой скорости – рад/с.
Вращение с постоянной угловой скоростью называется равномерным, при этом ω = φ/t.
Равномерное вращение можно характеризовать периодом обращения Т, под которым понимают время, за которое тело делает один оборот, т. е. поворачивается на угол 2π. Поскольку промежутку времени Δt = Т соответствует угол поворота Δφ = 2π, то
Число оборотов в единицу времени ν, очевидно, равно:
Величина ν измеряется в герцах (Гц). Один герц – это один оборот в секунду, или 2π рад/с.
Понятия периода обращения и числа оборотов в единицу времени можно сохранить и для неравномерного вращения, понимая под мгновенным значением T то время, за которое тело совершило бы один оборот, если бы оно вращалось равномерно с данным мгновенным значением угловой скорости, а под ν понимая то число оборотов, которое совершало бы тело за единицу времени при аналогичных условиях.
Если угловая скорость меняется со временем, то вращение называется неравномерным. В этом случае вводят угловое ускорение аналогично тому, как для прямолинейного движения вводилось линейное ускорение. Угловое ускорение – это изменение угловой скорости за единицу времени, вычисляется как производная угловой скорости по времени или вторая производная углового смещения по времени:
Так же, как и угловая скорость, угловое ускорение является векторной величиной. Вектор углового ускорения – аксиальный вектор, в случае ускоренного вращения направлен в ту же сторону, что и вектор угловой скорости (рис. 14); в случае замедленного вращения вектор углового ускорения направлен противоположно вектору угловой скорости.
При равнопеременном вращательном движении имеют место соотношения, аналогичные формулам (10) и (11), описывающим равнопеременное прямолинейное движение.
Движение по окружности - простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆ l = R ∆ φ
Если угол поворота мал, то ∆ l ≈ ∆ s .
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории - предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости - радиан в секунду (р а д с).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
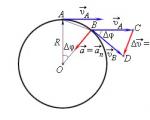
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → - v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → - v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
a n → = - ω 2 R → .
Здесь R → - радиус вектор точки на окружности с началом в ее центре.
В общем случае ускорение при движении по окружности состоит из двух компонентов - нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 - v 1 - изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Равномерное движение по окружности – это простейший пример . Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость .
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости в этом случае отсутствует (a r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение () a n или а ЦС. В каждой точке вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
a ЦС =v 2 / R
Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
360 о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958 о = 57 о 18’
Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω

Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
a ЦС = (4π 2 R) / T 2 = 4π 2 Rn 2