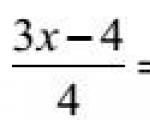Вычислить интеграл непосредственным интегрированием 2б. Непосредственное интегрирование
Поскольку сейчас речь пойдет только о неопределенном интеграле, то для сокращения термин «неопределенный» будем опускать.
Для того чтобы научиться вычислять интегралы (или, как говорят, интегрировать функции), нужно, прежде всего, выучить таблицу интегралов:
Таблица1. Таблица интегралов
|
2.
2a.
2б. 2в.
3.
3а.
4.
5.
5а) 6а.
7.
7а.
|
8.
9.
10.
10а.
11.
11а.
12.
13.
13а.
|
(
),
u
>0.
(α=0);
(α=1);
(α=
).
Кроме того, потребуется умение вычислять производную от заданной функции, а значит, нужно вспомнить правила дифференцирования и таблицу производных основных элементарных функций:
Таблица 2. Таблица производных и правила дифференцирования:
 6.а.
|
(sin и ) = cos и и (cos u ) = – sin и и |
|
А еще нам потребуется
умение находить дифференциал функции.
Напомним, что дифференциал функции
находят по формуле
,
т.е. дифференциал функции равен
произведению производной этой функции
на дифференциал её аргумента
. Полезно
держать в памяти и следующие известные
соотношения:
Таблица 3. Таблица дифференциалов
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
|
10.
11.
12.
14.
15.
16.
17.
|
(b
=
Const
)
(
)
(b
=
Const
)
Причем использовать эти формулы можно, как читая их слева направо, так и справа налево.
Рассмотрим последовательно три основных приема вычисления интеграла. Первый из них называют методом непосредственного интегрирования. Оноснован на использовании свойств неопределенного интеграла, включает два основных приема: разложение интеграла на алгебраическую сумму более простых и подведение под знак дифференциала , причем эти приемы могут быть использованы как самостоятельно, так и в совокупности.
А)
Рассмотрим
разложение на алгебраическую сумму
– этот прием предполагает использование
тождественных преобразований
подынтегральной функции и свойств
линейности неопределенного интеграла:
и
.
Пример 1. Найти интегралы:
а)
;
б)
;
в)
г)
д)
.
Решение.
а) Преобразуем подынтегральную функцию, разделив почленно числитель на знаменатель:
Здесь использовано
свойство степеней:
.
б) Сначала преобразуем числитель дроби, затем разделим почленно числитель на знаменатель:
Здесь также
использовано свойство степеней:
.
Здесь использовано
свойство:
,
.
.
Здесь использованы формулы 2 и 5 таблицы 1.
Пример 2. Найти интегралы:
а)
;
б)
;
в)
г)
д)
.
Решение.
а) Преобразуем подынтегральную функцию, используя тригонометрическое тождество :
.
Здесь вновь использовано почленное деление числителя на знаменатель и формулы 8 и 9 таблицы 1.
б)
Аналогично
преобразуем, используя тождество
:
.
в)
Сначала
разделим почленно числитель на знаменатель
и вынесем за знак интеграла константы,
затем используем тригонометрическое
тождество
:
г) Применим формулу понижения степени:
,
д) Используя тригонометрические тождества, преобразуем:
Б) Рассмотрим прием интегрирования, который называют подведением под знак дифференциала . В основе этого приема лежит свойство инвариантности неопределенного интеграла:
если
,
то для любой дифференцируемой функции
и
= и
(х
) имеет место:
.
Это свойство позволяет значительно расширить таблицу простейших интегралов, так как в силу этого свойства формулы таблицы 1 справедливы не только для независимой переменной и , но и в случае, когда и – дифференцируемая функция какой-либо другой переменной.
Например,
,
но и
,
и
,
и
.
Или
и
,
и
.
Суть метода заключается в выделении в заданном подынтегральном выражении дифференциала некоторой функции так, чтобы этот выделенный дифференциал вместе с остальным выражением составляли табличную формула относительно этой функции. В случае необходимости при таком преобразовании можно соответствующим образом добавлять константы. Например:
(в последнем примере записано ln(3 + x 2) вместо ln|3 + x 2 | , так как выражение 3 + x 2 всегда положительно).
Пример
3.
Найти
интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
.
Решение.
а) .
Здесь использованы формулы 2а, 5а и 7а таблицы 1, две последние из которых получены как раз путем подведения под знак дифференциала:
Интегрировать
функции вида
приходится очень часто в рамках вычисления
интегралов от более сложных функция.
Чтобы каждый раз не повторять описанные
выше действия, рекомендуем запомнить
соответствующие формулы, приведённые
в таблице 1.
.
Здесь использована формула 3 таблицы 1.
в) Аналогично, учитывая что , преобразуем:
.
Здесь использована формула 2в таблицы 1.
г)
.
д) ;
е)
.
ж) ;
з)
.
Пример 4. Найти интегралы:
а)
б)
в)
.
Решение.
а) Преобразуем:
Здесь так же использована формула 3 таблицы 1.
б)
Используем формулу понижения степени
:
Здесь использованы формулы 2а и 7а таблицы 1.
Здесь наряду с
формулами 2 и 8 таблицы 1 использованы и
формулы таблицы 3:
,
.
Пример 5. Найти интегралы:
а)
;
б)
в)
;
г)
.
Решение.
а)
Произведение
можно дополнить (см. формулы 4 и 5 таблицы
3) до
дифференциала функции
,
где а
и b
– любые константы,
.
Действительно,
,
откуда
.
Тогда имеем:
.
б)
Используя формулу 6 таблицы 3, имеем
,
а также
,
значит, присутствие в подынтегральном
выражении произведения
означает подсказку: под знак дифференциала
нужно внести выражение
.
Поэтому получаем
в) Так
же как в пункте б), произведение
можно дополнить до дифференциала
функции
.
Тогда получим:
.
г) Сначала воспользуемся свойствами линейности интеграла:
Пример 6. Найти интегралы:
а)
;
б)
;
в)
; г)
.
Решение.
а)
Учитывая,
что
(формула 9 таблицы 3), преобразуем:
б) Используя формулу 12 таблицы 3, получим
в) Учитывая формулу 11 таблицы 3, преобразуем
г) Используя формулу 16 таблицы 3, получим:
.
Пример 7. Найти интегралы:
а)
;
б)
;
в)
;
г)
.
Решение.
а) Все представленные в этом примере интегралы имеют общую особенность : подынтегральная функция содержит квадратный трехчлен. Поэтому и способ вычисления этих интегралов будет основан на одном и том же преобразовании – выделении полного квадрата в этом квадратном трехчлене.
.
б)
.
в)
г)
Прием подведения под знак дифференциала является устной реализацией более общего приема вычисления интеграла, называемого методом подстановки или заменой переменной. Действительно, каждый раз, подбирая подходящую формулу таблицы 1 к полученной в результате подведения под знак дифференциала функции, мы мысленно заменяли буквой и функцию, внесенную под знак дифференциала. Поэтому, если интегрирование путем подведения под знак дифференциала не очень получается, можно непосредственно делать замену переменной. Подробнее об этом – в следующем пункте.
Поскольку сейчас речь пойдет только о неопределенном интеграле, то для сокращения термин «неопределенный» будем опускать.
Для того чтобы научиться вычислять интегралы (или, как говорят, интегрировать функции), нужно, прежде всего, выучить таблицу интегралов:
Таблица1. Таблица интегралов
|
2.
2a.
2б. 2в.
3.
3а.
4.
5.
5а) 6а.
7.
7а.
|
8.
9.
10.
10а.
11.
11а.
12.
13.
13а.
|
(
),
u
>0.
(α=0);
(α=1);
(α=
).
Кроме того, потребуется умение вычислять производную от заданной функции, а значит, нужно вспомнить правила дифференцирования и таблицу производных основных элементарных функций:
Таблица 2. Таблица производных и правила дифференцирования:
 6.а.
|
(sin и ) = cos и и (cos u ) = – sin и и |
|
А еще нам потребуется
умение находить дифференциал функции.
Напомним, что дифференциал функции
находят по формуле
,
т.е. дифференциал функции равен
произведению производной этой функции
на дифференциал её аргумента
. Полезно
держать в памяти и следующие известные
соотношения:
Таблица 3. Таблица дифференциалов
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
|
10.
11.
12.
14.
15.
16.
17.
|
(b
=
Const
)
(
)
(b
=
Const
)
Причем использовать эти формулы можно, как читая их слева направо, так и справа налево.
Рассмотрим последовательно три основных приема вычисления интеграла. Первый из них называют методом непосредственного интегрирования. Оноснован на использовании свойств неопределенного интеграла, включает два основных приема: разложение интеграла на алгебраическую сумму более простых и подведение под знак дифференциала , причем эти приемы могут быть использованы как самостоятельно, так и в совокупности.
А)
Рассмотрим
разложение на алгебраическую сумму
– этот прием предполагает использование
тождественных преобразований
подынтегральной функции и свойств
линейности неопределенного интеграла:
и
.
Пример 1. Найти интегралы:
а)
;
б)
;
в)
г)
д)
.
Решение.
а) Преобразуем подынтегральную функцию, разделив почленно числитель на знаменатель:
Здесь использовано
свойство степеней:
.
б) Сначала преобразуем числитель дроби, затем разделим почленно числитель на знаменатель:
Здесь также
использовано свойство степеней:
.
Здесь использовано
свойство:
,
.
.
Здесь использованы формулы 2 и 5 таблицы 1.
Пример 2. Найти интегралы:
а)
;
б)
;
в)
г)
д)
.
Решение.
а) Преобразуем подынтегральную функцию, используя тригонометрическое тождество :
.
Здесь вновь использовано почленное деление числителя на знаменатель и формулы 8 и 9 таблицы 1.
б)
Аналогично
преобразуем, используя тождество
:
.
в)
Сначала
разделим почленно числитель на знаменатель
и вынесем за знак интеграла константы,
затем используем тригонометрическое
тождество
:
г) Применим формулу понижения степени:
,
д) Используя тригонометрические тождества, преобразуем:
Б) Рассмотрим прием интегрирования, который называют подведением под знак дифференциала . В основе этого приема лежит свойство инвариантности неопределенного интеграла:
если
,
то для любой дифференцируемой функции
и
= и
(х
) имеет место:
.
Это свойство позволяет значительно расширить таблицу простейших интегралов, так как в силу этого свойства формулы таблицы 1 справедливы не только для независимой переменной и , но и в случае, когда и – дифференцируемая функция какой-либо другой переменной.
Например,
,
но и
,
и
,
и
.
Или
и
,
и
.
Суть метода заключается в выделении в заданном подынтегральном выражении дифференциала некоторой функции так, чтобы этот выделенный дифференциал вместе с остальным выражением составляли табличную формула относительно этой функции. В случае необходимости при таком преобразовании можно соответствующим образом добавлять константы. Например:
(в последнем примере записано ln(3 + x 2) вместо ln|3 + x 2 | , так как выражение 3 + x 2 всегда положительно).
Пример
3.
Найти
интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
.
Решение.
а) .
Здесь использованы формулы 2а, 5а и 7а таблицы 1, две последние из которых получены как раз путем подведения под знак дифференциала:
Интегрировать
функции вида
приходится очень часто в рамках вычисления
интегралов от более сложных функция.
Чтобы каждый раз не повторять описанные
выше действия, рекомендуем запомнить
соответствующие формулы, приведённые
в таблице 1.
.
Здесь использована формула 3 таблицы 1.
в) Аналогично, учитывая что , преобразуем:
.
Здесь использована формула 2в таблицы 1.
г)
.
д) ;
е)
.
ж) ;
з)
.
Пример 4. Найти интегралы:
а)
б)
в)
.
Решение.
а) Преобразуем:
Здесь так же использована формула 3 таблицы 1.
б)
Используем формулу понижения степени
:
Здесь использованы формулы 2а и 7а таблицы 1.
Здесь наряду с
формулами 2 и 8 таблицы 1 использованы и
формулы таблицы 3:
,
.
Пример 5. Найти интегралы:
а)
;
б)
в)
;
г)
.
Решение.
а)
Произведение
можно дополнить (см. формулы 4 и 5 таблицы
3) до
дифференциала функции
,
где а
и b
– любые константы,
.
Действительно,
,
откуда
.
Тогда имеем:
.
б)
Используя формулу 6 таблицы 3, имеем
,
а также
,
значит, присутствие в подынтегральном
выражении произведения
означает подсказку: под знак дифференциала
нужно внести выражение
.
Поэтому получаем
в) Так
же как в пункте б), произведение
можно дополнить до дифференциала
функции
.
Тогда получим:
.
г) Сначала воспользуемся свойствами линейности интеграла:
Пример 6. Найти интегралы:
а)
;
б)
;
в)
; г)
.
Решение.
а)
Учитывая,
что
(формула 9 таблицы 3), преобразуем:
б) Используя формулу 12 таблицы 3, получим
в) Учитывая формулу 11 таблицы 3, преобразуем
г) Используя формулу 16 таблицы 3, получим:
.
Пример 7. Найти интегралы:
а)
;
б)
;
в)
;
г)
.
Решение.
а) Все представленные в этом примере интегралы имеют общую особенность : подынтегральная функция содержит квадратный трехчлен. Поэтому и способ вычисления этих интегралов будет основан на одном и том же преобразовании – выделении полного квадрата в этом квадратном трехчлене.
.
б)
.
в)
г)
Прием подведения под знак дифференциала является устной реализацией более общего приема вычисления интеграла, называемого методом подстановки или заменой переменной. Действительно, каждый раз, подбирая подходящую формулу таблицы 1 к полученной в результате подведения под знак дифференциала функции, мы мысленно заменяли буквой и функцию, внесенную под знак дифференциала. Поэтому, если интегрирование путем подведения под знак дифференциала не очень получается, можно непосредственно делать замену переменной. Подробнее об этом – в следующем пункте.
В этой теме мы подробно поговорим о свойствах неопределённого интеграла и о нахождении самих интегралов с помощью упомянутых свойств. Также поработаем с таблицей неопределенных интегралов . Материал, изложенный здесь, есть продолжение темы "Неопределённый интеграл. Начало" . Честно говоря, в контрольных работах редко встречаются интегралы, которые можно взять с использованием типичных таблиц и(или) простейших свойств. Эти свойства можно сравнить с азбукой, знание и разумение которой необходимы для понимания механизма решения интегралов в иных темах. Часто интегрирование с использованием таблиц интегралов и свойств неопределённого интеграла именуют непосредственным интегрированием .
К чему я веду: функции меняются, но формула для нахождения производной остаётся неизменной, - в отличие от интеграла, для которого уже пришлось перечислить два метода.
Пойдём дальше. Чтобы найти производную $y=x^{-\frac{1}{2}}\cdot(1+x^{\frac{1}{4}})^\frac{1}{3}$ применима всё та же формула $(u\cdot v)"=u"\cdot v+u\cdot v"$, в которую придётся подставить $u=x^{-\frac{1}{2}}$, $v=(1+x^{\frac{1}{4}})^\frac{1}{3}$. А вот чтобы найти интеграл $\int x^{-\frac{1}{2}}\cdot(1+x^{\frac{1}{4}})^\frac{1}{3} dx$ потребуется применение нового метода - подстановок Чебышева.
Ну и напоследок: для нахождения производной функции $y=\sin x\cdot\frac{1}{x}$ вновь применима формула $(u\cdot v)"=u"\cdot v+u\cdot v"$, в которую вместо $u$ и $v$ подставим соответственно $\sin x$ и $\frac{1}{x}$. А вот $\int \sin x\cdot\frac{1}{x} dx$ не берётся. Точнее, не выражается через конечное число элементарных функций.
Подведём итоги: там, где для нахождения производной понадобилась одна формула, для интеграла потребовались четыре (и это не предел), - причем в последнем случае интеграл находиться отказался вообще. Изменили функцию - понадобился новый метод интегрирования. Вот отсюда и имеем многостраничные таблицы в справочниках. Отсутствие общего метода (пригодного для решения "вручную") приводит к изобилию частных методик, которые применимы лишь для интегрирования своего, крайне ограниченного класса функций (в дальнейших темах мы займёмся этими методами подробно). Хотя не могу не отметить наличие алгоритма Риша (советую почитать описание в Википедии), но он пригоден лишь для программной обработки неопределённых интегралов.
Вопрос №3
Но если этих свойств так много, как же мне научиться брать интегралы? С производными было полегче!
Для человека пока существует лишь один способ: решить как можно больше примеров на применение различных методик интегрирования, чтобы при появлении нового неопределённого интеграла можно было подобрать для него метод решения, основываясь на своём опыте. Понимаю, что ответ не слишком обнадёживает, но иного нет.
Свойства неопределённого интеграла
Свойство №1
Производная от неопределенного интеграла равна подынтегральной функции, т.е. $\left(\int f(x) dx\right)"=f(x)$.
Это свойство вполне естественно, ибо интеграл и производная - взаимно обратные операции. Например, $\left(\int \sin 3x dx\right)"=\sin 3x$, $\left(\int \left(3x^2+\frac{4}{\arccos x}\right) dx\right)"=3x^2+\frac{4}{\arccos x}$ и так далее.
Свойство №2
Неопределённый интеграл от дифференциала некоторой функции равен этой функции, т.е. $\int \mathrm d F(x) =F(x)+C$.
Обычно данное свойство воспринимается несколько затруднительно, поскольку кажется, что под интегралом "ничего нет". Чтобы этого избежать, можно записать указанное свойство так: $\int 1\mathrm d F(x) =F(x)+C$. Пример применения этого свойства: $\int \mathrm d(3x^2+e^x+4)=3x^2+e^x+4+C$ или, если угодно, в такой форме: $\int 1\; \mathrm d(3x^2+e^x+4) =3x^2+e^x+4+C$.
Свойство №3
Постоянный множитель можно выносить за знак интеграла, т.е. $\int a\cdot f(x) dx=a\cdot\int f(x) dx$ (полагаем, что $a\neq 0$).
Свойство довольно простое и, пожалуй, комментариев не требует. Примеры: $\int 3x^5 dx=3\cdot \int x^5 dx$, $\int (2x+4e^{7x}) dx=2\cdot\int(x+2e^{7x})dx$, $\int kx^2dx=k\cdot\int x^2dx$ ($k\neq 0$).
Свойство №4
Интеграл суммы (разности) двух функций равен сумме (разности) интегралов от этих функций:
$$\int(f_1(x)\pm f_2(x))dx=\int f_1(x)dx\pm\int f_2(x)dx$$
Примеры: $\int(\cos x+x^2)dx=\int \cos xdx+\int x^2 dx$, $\int(e^x - \sin x)dx=\int e^xdx -\int \sin x dx$.
В стандартных контрольных работах обычно применяются свойства №3 и №4, вот на них мы и остановимся поподробнее.
Пример №3
Найти $\int 3 e^x dx$.
Используем свойство №3 и вынесем константу, т.е. число $3$, за знак инеграла: $\int 3 e^x dx=3\cdot\int e^x dx$. Теперь откроем таблицу интегралов и подставив в формулу №4 $u=x$ получим: $\int e^x dx=e^x+C$. Отсюда следует, что $\int 3 e^x dx=3\cdot\int e^x dx=3e^x+C$. Предполагаю, что тут сразу возникнет вопрос у читателя, поэтому сформулирую этот вопрос отдельно:
Вопрос №4
Если $\int e^x dx=e^x+C$, то $\int 3 e^x dx=3\cdot\int e^x dx=3\cdot\left(e^x+C\right)=3e^x+3C$! Почему вместо $3e^x+3C$ записали просто $3e^x+C$?
Вопрос совершенно разумен. Дело в том, что интегральную константу (т.е. то самое число $C$) можно представлять в виде любого выражения: главное, чтобы это выражение "пробегало" все множество действительных чисел, т.е. изменялось в пределах от $-\infty$ до $+\infty$. Например, если $-\infty≤ C ≤ +\infty$, то $-\infty≤ \frac{C}{3} ≤ +\infty$, поэтому константа $C$ представима в форме $\frac{C}{3}$. Можно записать, что $\int e^x dx=e^x+\frac{C}{3}$ и тогда $\int 3 e^x dx=3\cdot\int e^x dx=3\cdot\left(e^x+\frac{C}{3}\right)=3e^x+C$. Как видите, никакого противоречия здесь нет, но нужно соблюдать осторожность при изменении формы интегральной константы. Например, если представить константу $C$ в виде $C^2$, это будет ошибкой. Дело в том, что $C^2 ≥ 0$, т.е. $C^2$ не изменяется от $-\infty$ до $+\infty$, не "пробегает" все действительные числа. Точно так же будет ошибкой представлять константу в виде $\sin C$, потому что $-1≤ \sin C ≤ 1$, т.е. $\sin C$ не "пробегает" всех значений действительной оси. В дальнейшем этот вопрос оговаривать особо не будем, а станем просто писать константу $C$ для каждого неопределённого интеграла.
Пример №4
Найти $\int\left(4\sin x-\frac{17}{x^2+9}-8x^3 \right)dx$.
Используем свойство №4:
$$\int\left(4\sin x-\frac{17}{x^2+9}-8x^3 \right) dx=\int 4\sin x dx-\int\frac{17}{x^2+9}dx-\int8x^3dx$$
Теперь вынесем константы (числа) за знаки интегралов:
$$\int 4\sin x dx-\int\frac{17}{x^2+9}dx-\int8x^3dx=4\int \sin x dx-17\int\frac{dx}{x^2+9}-8\int x^3dx$$
Далее поработаем с каждым полученным интегралом по отдельности. Первый интеграл, т.е. $\int \sin x dx$, легко отыскать в таблице интегралов под №5. Подставляя в формулу №5 $u=x$ получим: $\int \sin x dx=-\cos x+C$.
Для нахождения второго интеграла $\int\frac{dx}{x^2+9}$ нужно применить формулу №11 из таблицы интегралов. Подставляя в неё $u=x$ и $a=3$ получим: $\int\frac{dx}{x^2+9}=\frac{1}{3}\cdot \arctg\frac{x}{3}+C$.
И, наконец, для нахождения $\int x^3dx$ используем формулу №1 из таблицы, подставив в неё $u=x$ и $\alpha=3$: $\int x^3dx=\frac{x^{3+1}}{3+1}+C=\frac{x^4}{4}+C$.
Все интегралы, входящие в выражение $4\int \sin x dx-17\int\frac{dx}{x^2+9}-8\int x^3dx$, найдены. Осталось лишь подставить их:
$$4\int \sin x dx-17\int\frac{dx}{x^2+9}-8\int x^3dx=4\cdot(-\cos x)-17\cdot\frac{1}{3}\cdot\arctg\frac{x}{3}-8\cdot\frac{x^4}{4}+C=\\ =-4\cdot\cos x-\frac{17}{3}\cdot\arctg\frac{x}{3}-2\cdot x^4+C.$$
Задача решена, ответ таков: $\int\left(4\sin x-\frac{17}{x^2+9}-8x^3 \right)dx=-4\cdot\cos x-\frac{17}{3}\cdot\arctg\frac{x}{3}-2\cdot x^4+C$. Добавлю всё же одно маленькое примечание к этой задаче:
Совсем маленькое примечание
Возможно, эта вставка никому не понадобится, но всё-таки упомяну, что $\frac{1}{x^2+9}\cdot dx=\frac{dx}{x^2+9}$. Т.е. $\int\frac{17}{x^2+9}dx=17\cdot\int\frac{1}{x^2+9}dx=17\cdot\int\frac{dx}{x^2+9}$.
Разберём пример, в котором используем формулу №1 из таблицы интегралов для интерирования иррациональностей (корней, проще говоря).
Пример №5
Найти $\int\left(5\cdot\sqrt{x^4}-\frac{14}{\sqrt{x^6}}\right)dx$.
Для начала проделаем те же действия, что и в примере №3, а именно: разложим интеграл на два и вынесем константы за знаки интегралов:
$$\int\left(5\cdot\sqrt{x^4}-\frac{14}{\sqrt{x^6}} \right)dx=\int\left(5\cdot\sqrt{x^4} \right)dx-\int\frac{14}{\sqrt{x^6}} dx=\\ =5\cdot\int\sqrt{x^4} dx-14\cdot\int\frac{dx}{\sqrt{x^6}} $$
Так как $\sqrt{x^4}=x^{\frac{4}{7}}$, то $\int\sqrt{x^4} dx=\int x^{\frac{4}{7}}dx$. Для нахождения данного интеграла применим формулу №1, подставив в нее $u=x$ и $\alpha=\frac{4}{7}$: $\int x^{\frac{4}{7}}dx=\frac{x^{\frac{4}{7}+1}}{\frac{4}{7}+1}+C=\frac{x^{\frac{11}{7}}}{\frac{11}{7}}+C=\frac{7\cdot\sqrt{x^{11}}}{11}+C$. При желании можно представить $\sqrt{x^{11}}$ как $x\cdot\sqrt{x^{4}}$, но это не обязательно.
Обратимся теперь к второму интегралу, т.е. $\int\frac{dx}{\sqrt{x^6}}$. Так как $\frac{1}{\sqrt{x^6}}=\frac{1}{x^{\frac{6}{11}}}=x^{-\frac{6}{11}}$, то рассматриваемый интеграл можно представить в такой форме: $\int\frac{dx}{\sqrt{x^6}}=\int x^{-\frac{6}{11}}dx$. Для нахождения полученного интеграла применим формулу №1 из таблицы интегралов, подставив в неё $u=x$ и $\alpha=-\frac{6}{11}$: $\int x^{-\frac{6}{11}}dx=\frac{x^{-\frac{6}{11}+1}}{-\frac{6}{11}+1}+C=\frac{x^{\frac{5}{11}}}{\frac{5}{11}}+C=\frac{11\cdot\sqrt{x^{5}}}{5}+C$.
Подставляя полученные результаты, получим ответ:
$$5\cdot\int\sqrt{x^4} dx-14\cdot\int\frac{dx}{\sqrt{x^6}}= 5\cdot\frac{7\cdot\sqrt{x^{11}}}{11}-14\cdot\frac{11\cdot\sqrt{x^{5}}}{5}+C= \frac{35\cdot\sqrt{x^{11}}}{11}-\frac{154\cdot\sqrt{x^{5}}}{5}+C. $$
Ответ : $\int\left(5\cdot\sqrt{x^4}-\frac{14}{\sqrt{x^6}}\right)dx=\frac{35\cdot\sqrt{x^{11}}}{11}-\frac{154\cdot\sqrt{x^{5}}}{5}+C$.
И, наконец, возьмём интеграл, подпадающий под формулу №9 таблицы интегралов. Пример №6, к которому мы сейчас перейдём, можно бы решить и иным способом, но об этом пойдёт речь в последующих темах. Пока что будем оставаться в рамках применения таблицы.
Пример №6
Найти $\int\frac{12}{\sqrt{15-7x^2}}dx$.
Для начала проделаем ту же операцию, что и ранее: вынесение константы (числа $12$) за знак интеграла:
$$ \int\frac{12}{\sqrt{15-7x^2}}dx=12\cdot\int\frac{1}{\sqrt{15-7x^2}}dx=12\cdot\int\frac{dx}{\sqrt{15-7x^2}} $$
Полученный интеграл $\int\frac{dx}{\sqrt{15-7x^2}}$ уже близок к табличному $\int\frac{du}{\sqrt{a^2-u^2}}$ (формула №9 таблицы интегралов). Отличие нашего интеграла в том, что перед $x^2$ под корнем стоит коэффициент $7$, которого табличный интеграл не допускает. Следовательно, нужно избавиться от этой семёрки, вынеся её за знак корня:
$$ 12\cdot\int\frac{dx}{\sqrt{15-7x^2}}=12\cdot\int\frac{dx}{\sqrt{7\cdot\left(\frac{15}{7}-x^2\right)}}= 12\cdot\int\frac{dx}{\sqrt{7}\cdot\sqrt{\frac{15}{7}-x^2}}=\frac{12}{\sqrt{7}}\cdot\int\frac{dx}{\sqrt{\frac{15}{7}-x^2}} $$
Если сравнить табличный интеграл $\int\frac{du}{\sqrt{a^2-u^2}}$ и $\int\frac{dx}{\sqrt{\frac{15}{7}-x^2}}$ становится видно, что они имеют одинаковую структуру. Только в интеграле $\int\frac{dx}{\sqrt{\frac{15}{7}-x^2}}$ вместо $u$ стоит $x$, а вместо $a^2$ стоит $\frac{15}{7}$. Что ж, если $a^2=\frac{15}{7}$, то $a=\sqrt{\frac{15}{7}}$. Подставляя $u=x$ и $a=\sqrt{\frac{15}{7}}$ в формулу $\int\frac{du}{\sqrt{a^2-u^2}}=\arcsin\frac{u}{a}+C$, получим такой результат:
$$ \frac{12}{\sqrt{7}}\cdot\int\frac{dx}{\sqrt{\frac{15}{7}-x^2}}= \frac{12}{\sqrt{7}}\cdot\arcsin\frac{x}{\sqrt{\frac{15}{7}}}+C $$
Если учесть, что $\sqrt{\frac{15}{7}}=\frac{\sqrt{15}}{\sqrt{7}}$, то результат можно переписать без "трёхэтажных" дробей:
$$ \frac{12}{\sqrt{7}}\cdot\arcsin\frac{x}{\sqrt{\frac{15}{7}}}+C=\frac{12}{\sqrt{7}}\cdot\arcsin\frac{x}{\frac{\sqrt{15}}{\sqrt{7}}}+C= \frac{12}{\sqrt{7}}\cdot\arcsin\frac{\sqrt{7}\;x}{\sqrt{15}}+C $$
Задача решена, ответ получен.
Ответ : $\int\frac{12}{\sqrt{15-7x^2}}dx=\frac{12}{\sqrt{7}}\cdot\arcsin\frac{\sqrt{7}\;x}{\sqrt{15}}+C$.
Пример №7
Найти $\int\tg^2xdx$.
Для интегрирования тригонометрических функций есть свои методы. Однако в данном случае можно обойтись знанием простых тригонометрических формул. Так как $\tg x=\frac{\sin x}{\cos x}$, то $\left(\tg x\right)^2=\left(\frac{\sin x}{\cos x}\right)^2=\frac{\sin^2x}{\cos^2x}$. Учитывая $\sin^2x=1-\cos^2x$, получим:
$$ \frac{\sin^2x}{\cos^2x}=\frac{1-\cos^2x}{\cos^2x}=\frac{1}{\cos^2x}-\frac{\cos^2x}{\cos^2x}=\frac{1}{\cos^2x}-1 $$
Таким образом, $\int\tg^2xdx=\int\left(\frac{1}{\cos^2x}-1\right)dx$. Раскладывая полученный интеграл на сумму интегралов и применяя табличные формулы, будем иметь:
$$ \int\left(\frac{1}{\cos^2x}-1\right)dx=\int\frac{dx}{\cos^2x}-\int 1dx=\tg x-x+C. $$
Ответ : $\int\tg^2xdx=\tg x-x+C$.
Этот метод сводится к интегрированию дифференциального уравнения изогнутой оси балки (9.1) при известном законе изменения изгибающих моментов М (х). Считая жесткость балки при изгибе постоянной (EJ z = const) и последовательно интегрируя уравнение (9.1), получим
В выражениях (9.5) и в дальнейшем для упрощения записи опущены индексы у моментов инерции и изгибающих моментов.
Выражения (9.5) позволяют получить аналитические законы изменения прогибов и углов поворота в балке. Входящие в (9.5) постоянные интегрирования С 1 и С 2 подлежат определению из кинематических граничных условий и условий сопряжения участков балки.
Кинематические граничные условия отражают характер закрепления (опирания) балки и ставятся относительно прогибов и углов поворота. Например, для шарнирно опертой балки (рис. 9.4) граничные условия характеризуют отсутствие прогибов на опорах: х = 0, х = /, v = 0. Для консольной балки (рис. 9.5) граничные условия характеризуют равенство нулю прогиба и угла поворота в жесткой заделке: х = 0, v = 0; ср = 0.
Условия сопряжения ставятся на границах участков с различными законами изменения изгибающих моментов. При отсутствии промежуточных шарниров и так называемых параллелограммных механизмов (ползунов) условия сопряжения заключаются в равенстве прогибов и углов поворота в сечениях слева и справа от границы участков, то есть они характеризуют непрерывность и гладкость изогнутой оси балки. Например, для балки на рис. 9.4 можно записать: х = а, и = и
При наличии п участков с различными законами изменения изгибающих моментов выражение для прогиба будет содержать 2п постоянных интегрирования. Используя граничные условия и условия сопряжения участков, можно получить систему 2п линейных алгебраических уравнений относительно этих постоянных. После определения всех постоянных интегрирования будут установлены законы изменения u(x) и ср(х) в пределах каждого участка балки. Рассмотрим примеры определения прогибов и углов поворота в балках с помощью метода непосредственного интегрирования.
Пример 9.1. Определим аналитические выражения для и(лс) и cp(x) в консольной балке, нагруженной равномерно распределенной нагрузкой (рис. 9.6), и вычислим значения этих величин на свободном конце.
Изгибающий момент в балке на всем ее протяжении изменяется по закону квадратной параболы:
Подставим это выражение в решение (9.5) и проинтегрируем его:
Использовав граничные условия, определим постоянные интегрирования:
Запишем окончательные выражения для прогибов и углов поворота в балке и определим значения этих величин на свободном конце:
Пример 9.2.
Для шарнирно опертой балки, нагруженной на конце сосредоточенной силой (рис. 9.7), определим выражения для у(х) и (р(х) и вычислим значения этих величин в характерных сечениях.
Эпюра М приведена на рис. 9.7. Изгибающие моменты имеют различные законы изменения на первом и втором участках балки. Интегрируем дифференциальное уравнение изогнутой оси в пределах каждого участка.
Первый участок (0 2а):
Второй участок (2а
Для определения четырех постоянных интегрирования С, С 2 , D x и D 2 ставим граничные условия и условия сопряжения участков:
Из условия сопряжения участков получаем равенство постоянных интегрирования на первом и втором участках: С { = D v С 2 = D T Использовав граничные условия, находим значения постоянных:
Запишем окончательные выражения для и(х) и ср(х) в пределах каждого участка:
В этих выражениях вертикальная черта с цифрой внизу соответствует границе каждого участка. В пределах первого участка v и ср определяются функциями, стоящими до вертикальной черты с цифрой 1, а в пределах второго участка - до вертикальной черты с цифрой 2, то есть всеми функциями.
Вычислим v и (р в характерных сечениях балки:
В пределах первого участка знак угла поворота изменяется на противоположный. Установим положение сечения, где угол поворота обращается в нуль:
В сечении х =x Q прогиб балки имеет экстремум. Вычисляем его значение:
Для сравнения определим величину прогиба балки в середине пролета:
Можно отметить, что экстремальный прогиб весьма незначительно (на 2,6%) отличается от прогиба в середине пролета.
Выполним числовой расчет при Р= 20 кН и а = 1,6 м. Подберем сечение балки в виде стального прокатного двутавра, приняв коэффициент надежности по нагрузке у^= 1,2, коэффициент условий работы у с = 1, расчетное сопротивление материала R = 210 МПа = = 21 кН/см 2 и модуль упругости стали Е- 2,1 10 4 кН/см 2 .
Принимаем 120, W z = 184 см 3 , J = 1840 см 4 .
Вычислим наибольшие значения угла поворота и прогиба в балке. Согласно СНиП расчет производим на действие нормативных нагрузок.
Из рассмотренного примера видно, что при наличии в балке нескольких участков с различными законами изменения изгибающих моментов метод непосредственного интегрирования становится громоздким и неудобным.
